Conor Deegan | Feistel Network in Python

Feistel Network in Python

Introduction

Feistel networks are a design scheme used to construct block ciphers. A lot of block ciphers use this scheme including DES, GOST, and Blowfish. In block ciphers constructed using a Feistel network, encryption and decryption are very similar operations - the only difference is the order in which the sub-keys are used (more on that soon).

Named after Horst Feistel, Feistel networks were first used commercially in the Lucifer cipher designed by IBM in 1973. The Lucifer cipher would eventually set the basis for DES (with changes added by the NSA).

This article explains how a Feistel network works and implements one using Python. It goes without saying that this code should not be used to secure information of any kind. This is purely for learning and is not designed to be secure.

Design

At its core, a Feistel network uses a round function to encrypt and decrypt data. The image below illustrates a single round of a Feistel network.

Feistel-Network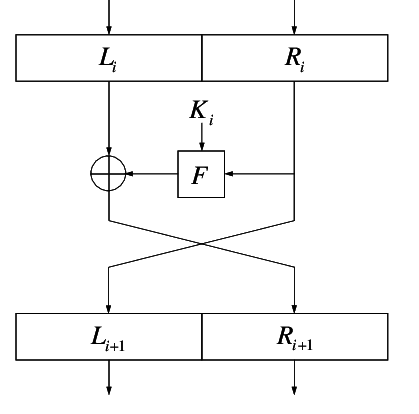-Single-Round Single round of a Feistel Network [4]

We can now step through the process of encryption using a Feistel Network. Let $F$ be the round function, $I_0$ be the first block of plaintext data, and $K_0, K_1,...,K_n$ be the sub-keys of $K$ for the rounds $0, 1,...,n$ respectively.

Before starting, $I_0$ is split into left and right halves such that $I_0 = (L_0 , R_0)$ .

For each round $i = 0,1,2...,n$ compute:

$L_{i+1} = R_i$

$R_{i+1} = L_i \oplus F(R_i, K_i)$

The ciphertext becomes $(R_{n+1} , L_{n+1})$

Decryption of the ciphertext $(R_{n+1} , L_{n+1})$ is computed by reversing $i=n, n-1, ...,0$ :

$R_i = L_{i+1}$

$L_i = R_{i+1} \oplus F(L_{i+1}, K_i)$

The plaintext becomes $(L_0 , R_0)$ - note this is what we stared with.

As can be seen above, a round function, $F$ , takes a block of input data and a subkey and produces an output of the same size as the input data. During each round, the round function runs on the right half of the input data and its output is XORed with the left half of the input data. This is repeated a number of times and the final output is the encrypted or decrypted string.

The function $F$ is what differentiates block ciphers that are based on a Feistel network. For instance, the logic contained within $F$ will be different in DES, GOST, Blowfish, etc. It is also what provides the security of the cipher. In the Python implementation below, the function $F$ simply XORs the input data with the subkey.

As can be seen, both the encryption and decryption operations are very similar, requiring only that the order of the sub-keys used is reversed. This is shown clearly in the diagram below.

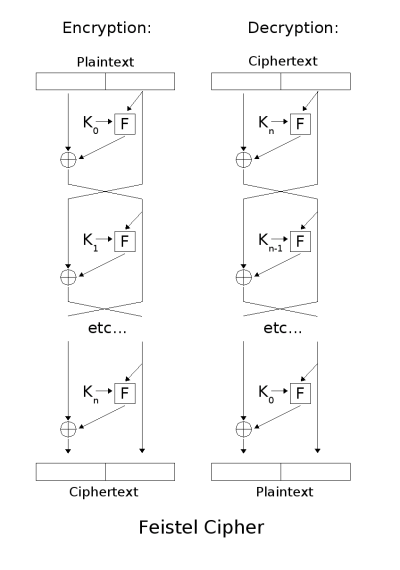Feistel-Network A Feistel Network with N rounds [3]

Python implementation

The full source code can be found here.

Although the code should be self-explanatory, I will briefly discuss the 3 most important functions; encrypt, decrypt, and round.

The encrypt function:

Takes 2 inputs; a plaintext sting, and a secret.

The plaintext string is converted into binary:

plaintext_bits = string_to_bits(plaintext)

This binary string is then split into blocks of 64 bits each. This is the block size for this Feistel network:

plaintext_blocks = split_to_blocks(plaintext_bits, 64)

A 265-bit key is then generated by hashing the secret provided using SHA-256:

key = generate_key(secret)

8 x 32bit sub-keys are then generated by splitting the key into 8 blocks of 32bits each:

sub_keys = split_to_blocks(key, 32)

Each block of plaintext is run through 8 rounds of the Feistel network. Once 8 rounds are completed, the resulting ciphertext block is stored.

for plaintext_block in plaintext_blocks:
  for i in range(8):
	  plaintext_block = round(plaintext_block, sub_keys[i])
  ciphertext_blocks.append(str(plaintext_block[32:]) + str(plaintext_block[:32]))

Once all ciphertext blocks have been computed, the function returns the entire ciphertext in hexadecimal format:

return bits_to_hex(''.join(ciphertext_blocks))

The round function:

The round function $F$ for this Feistel network simply XORs the sub-key with the right hand of the plaintext bits provided. The result of this is then XORed with the left hand bits. The halves are then swapped and returned.

def round(bits, sub_key):
    left_bits = bits[:32]
    right_bits = bits[32:]
    f_out = xor(sub_key, right_bits)
    left_xor_f_out = xor(left_bits, f_out)
    return right_bits + left_xor_f_out

The decrypt function:

The decryption function is almost identical to the encryption function. The only differences are that the ciphertext input to the function is a hexadecimal string and when performing the 8 rounds in order to decrypt the ciphertext, the sub-key order is reversed:

for ciphertext_block in ciphertext_blocks:
  for i in range(ROUNDS, 0, -1):
      ciphertext_block = round(ciphertext_block, sub_keys[i - 1])
  plaintext_blocks.append(str(ciphertext_block[32:]) + str(ciphertext_block[:32]))

Finally, when the recovered plaintext bits are combined, they are split into blocks of 8bits (1 byte) each in order to recover the original ASCII character.

References

Feistel Cipher - Computerphile
Feistel cipher - Wikipedia
Image source: By Feistel_cipher_diagram.svg: Amirkiderivative work: Amirki (talk) - Feistel_cipher_diagram.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16419258
Hernandez-Castro, J.C., Estevez-Tapiador, J.M., Ribagorda-Garnacho, A. and Ramos-Alvarez, B., 2006, July. Wheedham: An automatically designed block cipher by means of genetic programming. In 2006 IEEE International Conference on Evolutionary Computation (pp. 192-199). IEEE.

Note: these references exclude hyperlinks included throughout the document.

Disclaimer: Do not use this to secure any information. This code is purely to be used for educational purposes only.

← Back